Vitruvio,  Leonardo Da Vinci, el número Pi y la cuadratura del círculo.

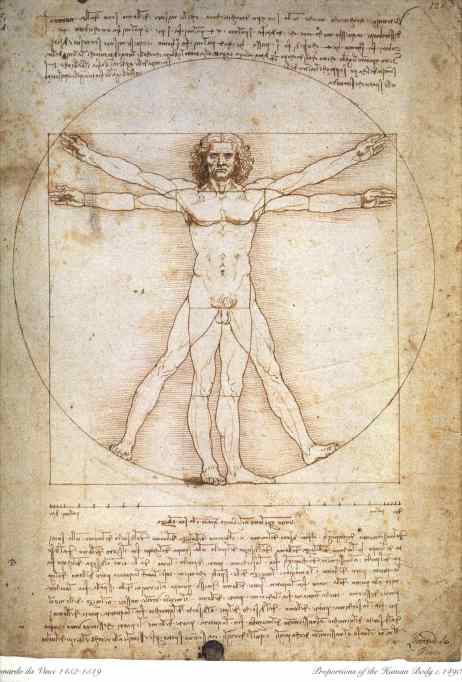
Figura 1

“El centro del cuerpo humano es el ombligo, de tal modo que en un hombre tendido en decúbito supino, con las manos y los pies extendidos, si se tomase como centro el ombligo, trazando con el compás un círculo, éste tocaría los dedos de ambas manos y los de los pies; y lo mismo que se adapta el cuerpo a la figura redonda , se adapta también a la cuadrada: por eso, si se toma la distancia que hay de la punta de los pies a lo alto de la cabeza, y se confronta con la de los brazos extendidos, se hallará que la altura y la anchura son iguales, resultando el cuadrado perfecto.”            “Igualmente porque el pie del hombre corresponde a la sexta parte de la altura de su cuerpo, o en otros términos, porque la expresión de la altura de su cuerpo en número de pies es este número, que es el de pies de la altura, estos resultan seis, declararon (los antiguos matemáticos) al seis numero perfecto; y también observaron que la longitud del codo se compone de seis palmos, y por consiguiente de veinticuatro dedos”.   Vitruvio, Libro III. Capítulo I.

Antecedentes:

 Vitruvio, arquitecto romano contemporáneo del emperador Augusto, autor del tratado de diez libros llamado “De Architectura”,  en su Libro III, capítulo I, nos presenta las diferentes unidades  de longitud romanas. Explica que todas ellas están basadas en las partes adecuadamente proporcionadas del cuerpo humano, (un pie son cuatro manos, una mano cuatro dedos, un codo equivale a un pie y medio, ...)

 Ver: http://www.fh-augsburg.de/~harsch/Chronologia/Lsante01/Vitruvius/vit_intr.html

 La dimensión equivalente estimada para un pie, unidad básica de longitud aplicada por los romanos, sería la de 0,296 metros, medida contrastada por numerosos autores, por ejemplo -ADAM, J. P. 1984: La construction romaine. Materiaux et techniques. Grands Manuels Picard, París (Ed. español 1996, León). o por -PANERAI, Mª C., 1983: Le misure romane, A.A.V.V., Misurare la terra: centuriazione e coloni nel mondo romano. Catálogo de la exposición de Modena, 11 de Septiembre 1983 a 12 de Febrero 1984, p. 122-124. Edizioni Panini, Modena.

 A su vez, determinados textos nos revelan que la dimensión denominada “pasus”, múltiplo equivalente a 5 pies, mide 1,481 metros, de lo cual deducimos que 1,481 m: 5  = 0,2962 m/pie, aproximándonos un decimal más en la medida del pie romano.

 Vitruvio, en el citado texto, nos define como módulo-hombre perfecto aquel que se inscribe en un cuadrado de 6 por 6 pies, es decir, que el hombre perfecto mide seis pies desde los pies a la cabeza, y seis pies de punta a punta de los dedos de las manos con los brazos extendidos.  A su vez menciona en ese capítulo que este mismo hombre, tomando como centro el ombligo, es inscribible en un círculo, tal como lo representó Leonardo Da Vinci en un conocido grabado. 

Ver Figura 1.

  Podemos entender que, en cierta manera, Vitruvio nos está diciendo que este módulo-hombre perfecto es no sólo un modulador de dimensiones a escala humana (mano, dedo, codo, pie...) utilizadas después mediante múltiplos  tanto en la construcción como en la medición de caminos, campos , etc,  sino que a la vez se constituye en el centro o síntesis geométrica del cuadrado y del círculo, es decir, el ser humano es el punto central de referencia donde se verificaría una propiedad geométrica aparentemente inalcanzable: la cuadratura del círculo. Inalcanzable desde nuestro actual conocimiento científico, porque el valor de Pi hoy conocido, al ser un número irracional trascendente con infinitos decimales no permite su trazado gráfico ni por tanto alcanzar la cuadratura.

 Pero cabe preguntarse si esta propiedad podría verificarse en esas épocas, ya que en ellas se trabajaba con otro valor de Pi obtenido por aproximaciones mucho más sencillas y ciertamente trazables geométricamente como pretendo demostrar, con lo que se entendería el empeño de Vitruvio de sintetizar en torno al módulo-hombre ambas figuras, cuadrado y círculo.

 Podemos iniciar la investigación  a partir del  análisis del valor de Pi o, mejor dicho,  de los dos posibles valores conocidos en la época, intentando relacionar estas aproximaciones con la dimensión del pie romano y a su vez concluir acerca de una posible explicación de la figura del Módulo-Hombre de Vitruvio.

1. Análisis en función del valor de Pi según el papiro egipcio de Ahmes:

       El primer valor de Pi del que Vitruvio debía tener conocimiento es el que se encuentra establecido por la geometría egipcia, contenido en el papiro de Ahmes, escriba-geómetra autor del mismo  en fecha 1650 antes de Cristo. También se le conoce como Papiro de  Rhind (denominado así por su descubridor). En este papiro se analiza la resolución de varios problemas geométricos y matemáticos y, entre ellos, se analiza el cálculo del área de un círculo de diámetro 9 por igualación con el área del cuadrado de lado 8. Se trata de una primera aproximación a la famosa cuadratura del círculo, ya que según Ahmes  tienen igual área el cuadrado de lado “L” y la circunferencia de diámetro “8L/9”.  Es decir, según este papiro, al considerar como igual el área del cuadrado de 8 x 8 = 64 y la del círculo de radio 4,5,  se puede deducir un valor de Pi = (16/9)² . En este caso el área del círculo vale igualmente A = (16/9)² x 4,5 x 4,5 = 64. Por tanto  Pi = (1.77777777...)²  = 3.1604935...  valor que difiere del actual pero que en su día debió representar un gran avance técnico para el cálculo de áreas circulares.

 Ver: http://www.egiptologia.org/ciencia/matematicas/papiro_rhind.htm

 Este valor de raíz cuadrada de Pi se puede asociar con el valor obtenido al multiplicar por 6 el valor del pie romano antes mencionado 6 x 0.296 = 1.776, o también el más aproximado 6 x 0.2962 = 1.7772. De aquí podemos establecer la siguiente hipótesis de trabajo: Si el valor equivalente en metros de un pie romano fuera realmente  0.296296296296... seis pies medirían 1.77777777... y por tanto la raíz cuadrada de Pi se podría expresar en pies:  trazando en el suelo seis pies tendríamos dibujado el lado del cuadrado del módulo-hombre, cuya área expresada en  metros cuadrados valdría Pi ya que Raíz cuadrada de Pi x Raíz cuadrada de Pi = Pi  Debemos tener en cuenta que en aquellos momentos el metro como unidad no existe, por lo que llama la atención esta coincidencia. Para intentar aclarar este misterio, vamos a trabajar con geometría, puesto que lo que se pretende demostrar a continuación es que el Pi egipcio puede ser trazado, para luego darle las proporciones adecuadas al módulo-hombre mediante un cambio de escala.

 Veamos la demostración: La definición de raíz cuadrada de Pi según Ahmes es un valor sencillo: 16/9. Esto es lo  mismo que 4²/3², lo cual  podemos asociarlo con las dimensiones del  triángulo pitagórico 3:4:5, imprescindible para el trazado de figuras con un ángulo recto, ya conocido por los egipcios y mencionado por Vitruvio en su Introducción al Libro IX de De Architectura.

:

Si a cualquier escala construimos un triángulo rectángulo con catetos de valor 9 y 16, apoyado sobre la base de 9, podemos trazar un triángulo semejante al anterior nueve veces menor de forma que el cateto base medirá 1 y el cateto vertical valdrá exactamente 16/9, es decir,  raíz cuadrada dePi. Por tanto es posible llegar a trazar gráficamente este valor de raíz de Pi,  siempre referidos al Pi egipcio, de la misma forma que con triángulos semejantes es posible dividir un segmento en tres partes iguales y obtener así para cada parte el valor 0.3333... segmento posible de dibujar e imposible de medir.        A partir de esta figura podemos dibujar  un cuadrado uno de cuyos lados sea el cateto de valor raíz cuadrada de Pi cuya área será, evidentemente, A = raíz de Pi x raíz de Pi =  Pi. Y a la vez podemos trazar un círculo cuyo radio sea  el cateto menor, de valor 1, cuya área será igualmente  A = Pi x 12 = Pi. Con lo que queda demostrada la posibilidad de que, con este valor aproximado de Pi era perfectamente posible en esa época  trazar la “cuadratura” del círculo. 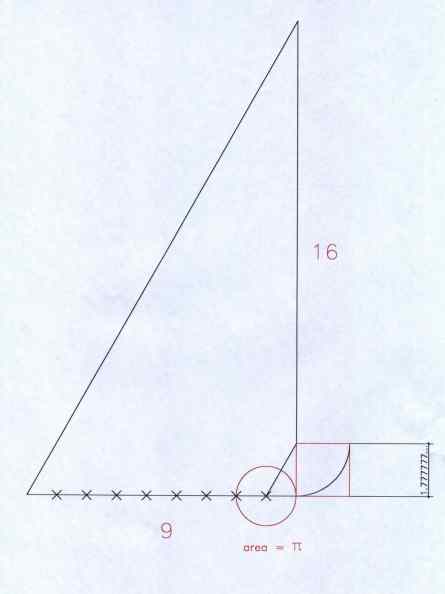Ver Figura 2	Figura 2
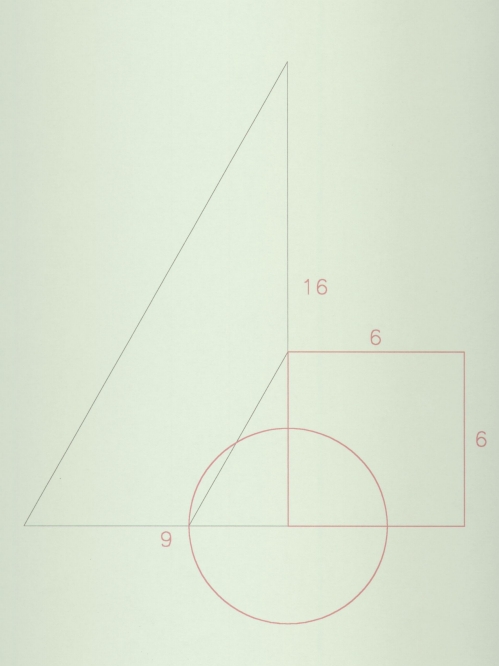Figura 3	Todo este desarrollo se ha realizado geométricamente, trabajando con unidades gráficas sin emplear un módulo o escala concreto (metros, pies,...) y el resultado es la definición de un módulo gráfico que es la raíz de Pi, = 1,77777777...  el cual, mediante un cambio de escala puede ser adaptado a cualquier tamaño.  De nuevo podemos recordar ahora a Vitruvio y su módulo-hombre, que pretende estar simultáneamente inscrito en un cuadrado y en un círculo, presumiblemente de áreas iguales. Podemos dibujar ambas figuras. Repitamos el análisis de los triángulos semejantes, suponiendo ahora que trabajamos en pies, sin que sea necesario previamente definir exactamente las dimensiones del pie en relación al metro, sino tan sólo dando importancia a que el módulo-hombre son seis pies.  Podemos realizar una nueva figura a partir de las proporciones del triángulo rectángulo de catetos 16:9, para crea una figura semejante cuyo cateto mayor valga 6. Según esto la relación proporcional es:                     16 es a 9 como 6 es a ...3,375.  Podemos comprobar que un cuadrado de lado 6 pies tiene la misma área que un círculo de radio 3,375 pies. Ver Figura 3.
Efectivamente:   Área del cuadrado: 6 x 6 = 36               Area del círculo = (16/9)2 x 3,375 x 3,375 = 36  Obtenemos así la cuadratura relativa a la figura mencionada por Vitruvio. En este caso el tamaño del círculo no sería exactamente el que trazó Leonardo da Vinci en su grabado, sino un poco menor, como vemos en la Figura 4. Aquí observamos que el Hombre con los brazos extendidos horizontales y las piernas abiertas encaja simultáneamente en el cuadrado y en el círculo, ambos de áreas iguales en base al Pi egipcio. ¿Era esto lo que nos quería decir Vitruvio?.   La relación entre ambas figuras geométricas tiene otras características curiosas:  hemos visto que el área del cuadrado de lado 8 equivale a l círculo de diámetro 9. La relación es Lado x 1,125 = diámetro. (8 x 1,125 = 9). En la relación entre “perímetros” el coeficiente que los relaciona es el mismo, pero situado a la inversa:   Perímetro cuadrado = Circunferencia x 1,125. Efectivamente,  4 x 8 =  (16/9)2 x 9 x 1,125.   Esto es válido para todos los cuadrados y circunferencias que cumplan las proporciones de 8:9 entre lado y diámetro.

En relación a su trazado gráfico, podemos trabajar aquí también con triángulos semejantes: si dibujamos un triángulo rectángulo de catetos 22 y 7, podemos dibujar un triángulo semejante en el que al lado de dimensión 7 del mayor le corresponda un lado de dimensión 1 en el menor. Así, el lado proporcional al cateto de valor 22 le corresponderá otro cateto en el triángulo menor cuyo valor será 22/7, es decir, Pi.   Pero este trazado no nos permite un inmediato trazado de la cuadratura del círculo, ya que en el caso anterior lo que habíamos obtenido gráficamente era la raíz cuadrada de Pi, lo cual nos permitía dibujar fácilmente un cuadrado cuya área era Pi. En este caso lo que sí podemos hacer es dibujar un rectángulo cuya base sea 1 y su altura Pi, con lo que el área valdrá Pi x 1 = Pi. A la vez, si dibujamos un círculo de radio igual a 1, su área valdrá Pi x 12 = Pi. Hemos conseguido la “rectangulatura” del círculo con el Pi de Arquímedes. .  Ver Figura 5.

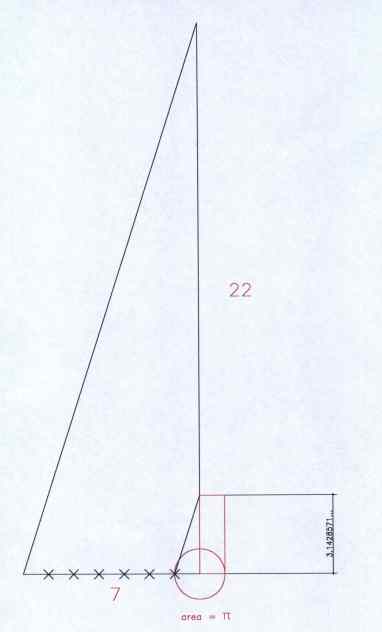
Figura 5

Para transformar este rectángulo en un cuadrado equivalente, aplicamos una regla geométrica basada en la media proporcinal:     http://trazoide.com/equivalencia.html

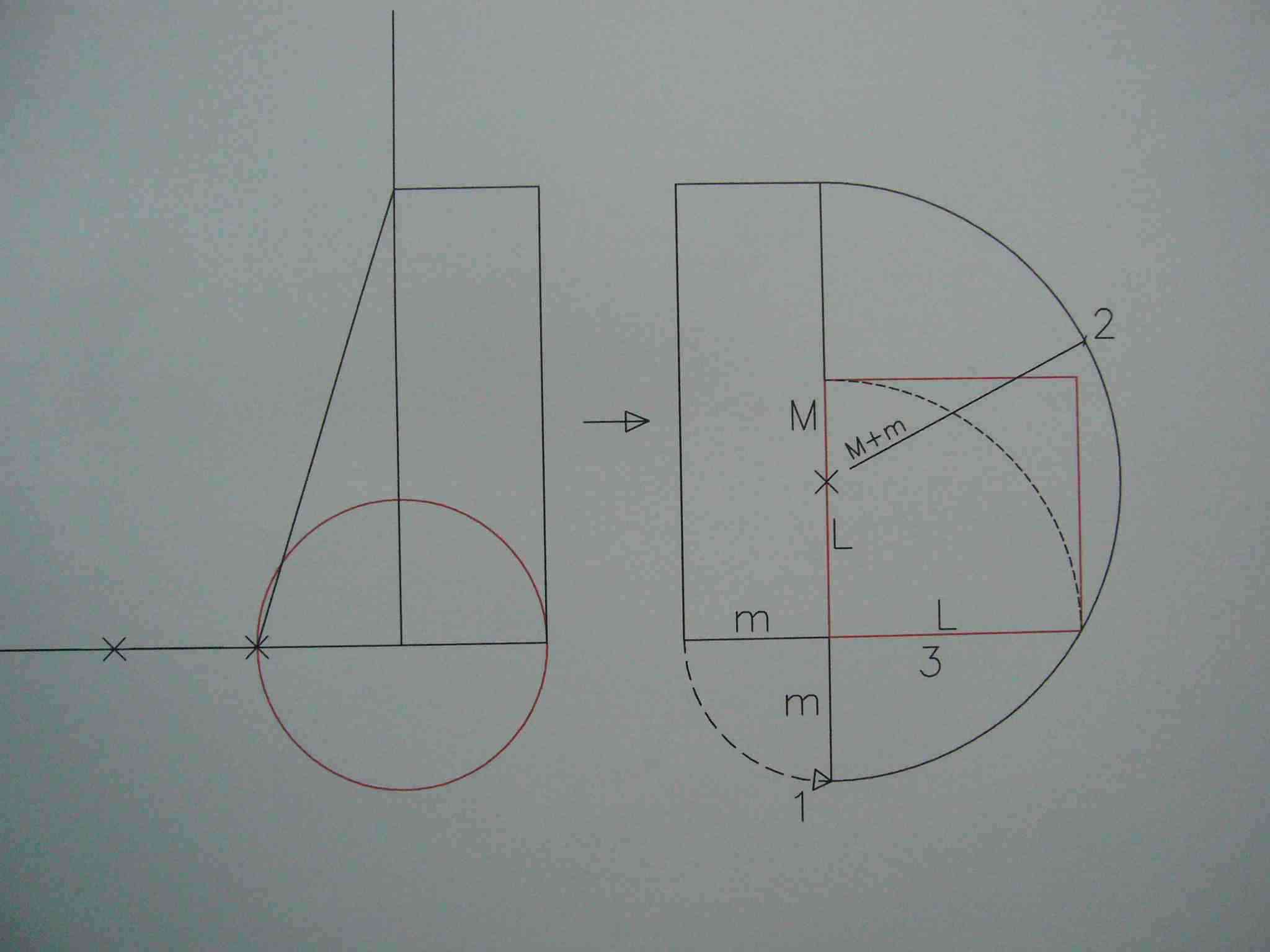
Figura 6

Entramos en el análisis de un nuevo posible valor del pie romano. Si aceptamos que Pi es 22/7 = 3.1428571, su raíz cuadrada valdrá 1.7728105. La sexta parte es 0.295468, valor que en metros es muy similar al del pie romano aplicado en otras obras arquitectónicas, el Templo de Gabii, por ejemplo: 0.2955 m.  ( Ver: Metrología y modulación del templo de Juno Gabina. Martín Almagro-Gorbea y José Luis Jiménez. Itálica. Cuadernos de Trabajo de la Escuela de Historia y Arqueología de Roma. 16. 1982. CSIC. Madrid.) De nuevo observamos que, curiosamente, si “leemos” en metros la medida de seis pies, ésta  de nuevo coincide con la raíz cuadrada de Pi, y por tanto a su vez  la nueva  área del cuadrado del “modulo-hombre” de 6 por seis pies, medido en metros cuadrados nos da el valor del Pi de Arquímedes.  Podemos pues pensar que se produce una readaptación del módulo–hombre en base a la nueva aproximación a Pi. Será interesante analizar la diferente utilización de estas medidas, para ver si efectivamente en general el pie de 0.2963 precede en el tiempo al de 0.2955, o si ambos coexisten.  Aquí tenemos tarea para los arqueólogos. En este caso se rompe la modulación con respecto a la circunferencia de la tierra.

Una consideración más sobre la modulación 6x6

Es interesante la referencia que hace Vitruvio en la Intruducción al Libro V sobre el número 216 como “numero cúbico”, tomada de Pitágoras:  Un cubo tiene 6 caras, número perfecto. Si el hombre de Vitruvio se inscribe en un cuadrado de 6 x 6 pies, resulta que la superficie envolvente de un cubo de lado 6 pies es (6 x 6) x 6, es decir, 216 pies cuadrados.

 A su vez, su volumen, B x H =  36 x 6 = 216 pies cúbicos.  Curiosa propiedad del cubo de lado 6, ya que realmente es el único cubo que admite esta propiedad:

S  = V   por tanto 6 L² = L³  es decir,  L=6

 No contentos con esto, si observamos la esfera inscribible en este cubo, que tendrá R= 3, es la única en la que se cumple igualmente que su área es igual a su volumen:

Para que S = V;   4 Pi r² =  4/3 Pi r³  por tanto,  1 = 1/3 r;  es decir,  r = 3 

Al hablar del cubo de lado 6, del Hombre inscribible en un cuadrado de  6,x,6 ¿nos están señalando tanto los  Pitagóricos como Vitruvio la cincidencia entre perfección geométrica y humana? ¿Es el Hombre la escala de la perfección?

 Veamos a la vez qué nos dice un libro escrito unos 100 años despues, en época en la que la teoría del 6x6 vitruviano estaría en vigor, el Apocalipsis de San Juan.

Según Apocalipsis, 13,18:

 “Aquí se debe aplicar la sabiduría. Quien se sienta inteligente pruebe a descifrar el número de la Bestia, que es número humano: seis, seis, seis”

 Según la traducción realizada por el P. Xavier Pikaza en su libro “Apocalipsis”, pg 156 y ss. Ed. Verbo Divino. 1999, no es del todo correcto traducir  666, (“seiscientos” “sesenta” y “seis”, tres palabras diferentes), sino que el texto parece que repite tres veces consecutivas la misma palabra “seis”: 6.6.6

San Juan nos habla por tanto de la asociación de un mismo número 6 repetido tres veces, a modo de una serie, situación coincidente con el uso del 6 de Vitruvio, que define el alto (6) y ancho (6) del hombre Vitruviano, el cuadrado que lo envuelve (6x6) , y el cubo que ayuda a contener la sabiduría (6x6x6).

Recordemos que la Segunda Bestia a la que se refiere el número 6-6-6 es, según los exégetas, nada menos que la cultura opresora al servicio del Imperio Romano (X.Picaza, “Apocalipsis”, pg 154-155).

 Si finalmente acudimos de nuevo al Apocalipsis, Capitulo 21,17, relativo a la Ciudad Santa que baja delñ cielo, la Nueva Jerusalén, nos dice S.Juan: "Y midió luego la muralla y resultaron ciento cuarenta y cuatro codos, según la medida humana, que es medida de ángel”.

 Un codo son 1,5 pies, luego 144 codos son 216 pies, es decir, 6 x 6 x 6. Nos aparece aquí de nuevo una relación entre una aplicación de las cifras 6-6-6 y la mención a la “medida humana”, comparándola a la "medida de angel” es decir, de nuevo aparece una invocación a la perfección.

 Quizás para San Juan la aparición de una regla de perfección humana basada en el número 6, perfectamente conocida en su época, significaba un peligro contra la religión cristiana al pretender elevar al Hombre a la cúspide de la perfección olvidando a Dios, de ahí que en el capítulo 21 busque subordinar ese Hombre Perfecto, modulador de edificios y ciudades proporcionadas en base a su cuerpo, a un Angel y a una Ciudad Nueva que procede de Dios. 

Luis Moranta Jaume, Arquitecto, Mayo 2001- Enero 2009.

Listado de direcciones de interés:                

Sobre Vitruvio:

http://www.fh-augsburg.de/~harsch/Chronologia/Lsante01/Vitruvius/vit_intr.html
http://firewall.unesco.org/webworld/nominations/fr/spain/espagne_vitruvenom.htm
http://ccat.sas.upenn.edu/george/vitruvius.html